Welche Stückzahl eines Artikels sollte jeweils auf einmal bestellt werden, um ökonomisch zu wirtschaften? Wird häufig bestellt, dafür aber stets kleine Mengen, dann steigt der Bestellaufwand ins Unermessliche. Wird hingegen selten bestellt, dafür aber jeweils große Mengen, dann fallen hohe Kosten für die Lagerhaltung an und es wird viel Kapital gebunden. Die optimale Bestellmenge muss demnach irgendwo dazwischen liegen.
Wir betrachten nun ein Modell, das als „klassische Losformel“ oder „Andler-Formel“ bekannt ist. Es wurde ursprünglich zur Ermittlung der optimalen Größe von Fertigungslosen entwickelt, lässt sich aber ebenso zur Ermittlung der optimalen Bestellmenge nutzen.
Das Ziel ist es, die jährlichen Kosten \( K \) in Abhängigkeit von der Bestellmenge \( x \) eines Artikels darzustellen, also \( K(x) \). An dem Punkt, an dem diese Funktion ihr Minimum hat, liegt die optimale Bestellmenge.
\begin{align} K &= jährliche \ Bestellkosten \\ x &= Bestellmenge \ des \ Artikels \\ B &= Kosten \ je \ Bestellung \\ j &= benötigte \ Jahresmenge \ des \ Artikels \\ l &= Lagerkostensatz \\ P &= Preis \ des \ Artikels \end{align}
Schritt 1: Die Fixkosten je Bestellung
Widmen wir uns zunächst den oben erwähnten Kosten, die für jede Bestellung anfallen – diese umfassen die Kosten für die komplette Bestellabwicklung im Einkauf (von der Bestellung bis zur Rechnungsprüfung), die Versandkosten sowie die Kosten für Warenannahme und Einlagern der Ware. Diese Kosten je Bestellung bezeichnen wir als \( B \) und nehmen an sie seien für den jeweiligen Artikel konstant, also unabhängig von der bestellten Menge. Die benötigte Jahresmenge des Artikels bezeichnen wir als \( j \). Die jährlich anfallenden Kosten für die Bestellungen des Artikels betragen also \[ Jährl. \ Kosten \ je \ Bestellung = \frac{j}{x} \cdot B \]
Ein kleines Beispiel zum Verständnis: Die benötigte Jahresmenge eines Artikels betrage \( j \) = 200 Stück. Es werden jeweils \( x \) = 50 Stück auf einmal bestellt. Demnach gibt es \( \frac{j}{x} \) = 4 Bestellungen pro Jahr. Geht man von Bestellkosten \( B \) = 150 € aus, dann betragen die jährlichen Bestellkosten in diesem Fall 600 €. In Abbildung 1 ist eine grafische Darstellung zu sehen. Daran ist zu erkennen, dass die jährlichen Kosten je Bestellung ins Unermessliche gehen, wenn die Bestellmenge gering ist.
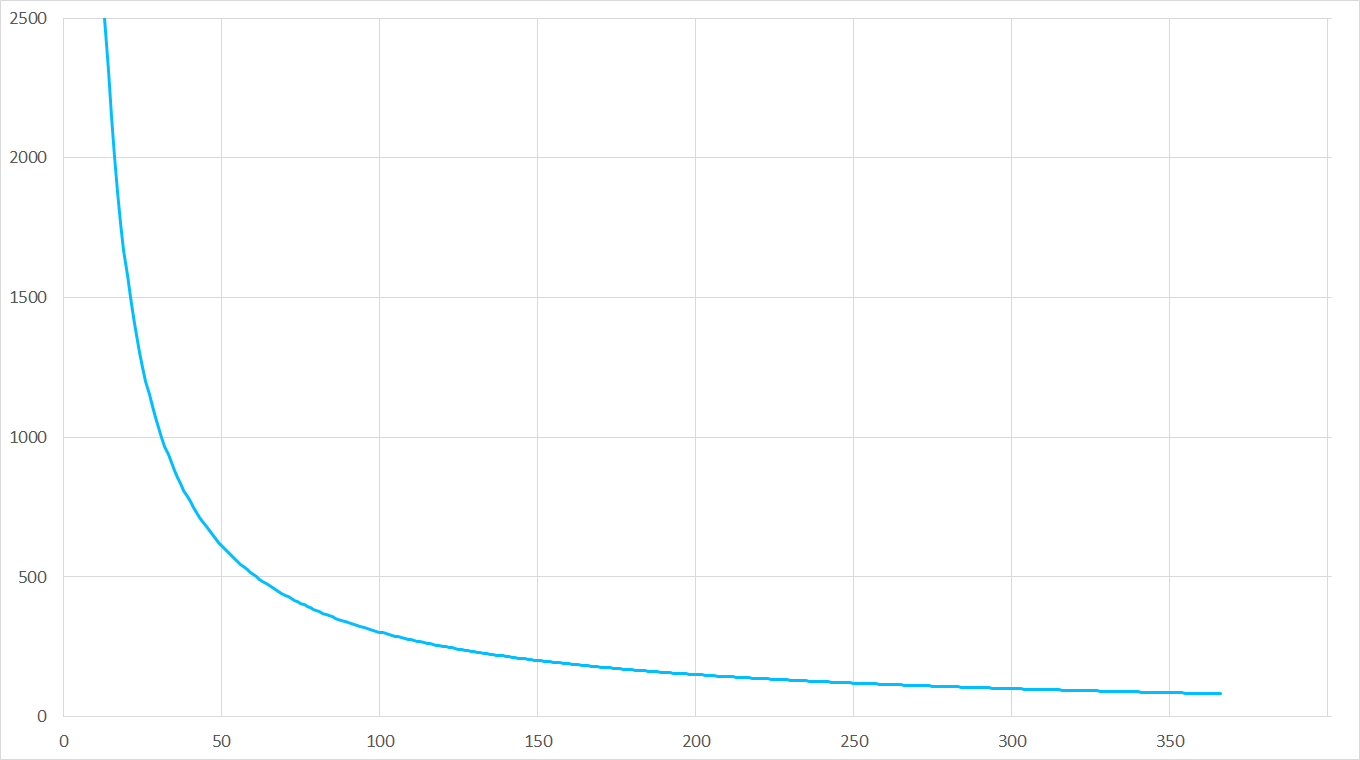
Abbildung 1: Jährliche Kosten je Bestellung in Abhängigkeit von der Bestellmenge
Schritt 2: Die Lagerhaltungskosten
Nun betrachten wir die Kosten, die für die Lagerung anfallen. Hierzu führen wir den Lagerkostensatz \( l \) ein, wobei \[ l = \frac{Lagerkosten}{\varnothing \ Lagerbestand} + Kapitalzinssatz \]
Der erste Term auf der rechten Seite des Gleichheitszeichens, also \( \frac{Lagerkosten}{\varnothing \ Lagerbestand} \), gibt an, welcher Prozentsatz des Artikelwertes für die Lagerhaltung anfällt. Beträgt er beispielsweise 10%, dann fallen für einen Artikel im Wert von 20 € jährliche Lagerkosten in Höhe von 2 € an. Die Kosten der Lagerhaltung hängen in diesem Modell demnach ausschließlich vom Artikelpreis ab und nicht beispielsweise von den Abmaßen des Artikels.
Addiert man zu diesem Wert den für das Unternehmen geltenden Kapitalzinssatz, z.B. 5%, dann erhält man den Lagerkostensatz \( l \), in unserem Beispiel wäre also \( l \) = 10% + 5% = 0,15.
Wenn \( P \) den Preis des zu betrachtenden Artikels bezeichnet, dann ergibt sich für die jährlichen Kosten der Lagerhaltung \[ Jährl. \ Lagerhaltungskosten = \frac{x \cdot P \cdot l}{2} \]
\( x \cdot P \) stellt den Wert der bestellten Ware dar. Geht man von einem kontinuierlichen Verbrauch aus sowie sofortigem Auffüllen des Artikels bei Bestand Null aus, dann beträgt der durchschnittliche Wert des auf Lager befindlichen Artikels genau die Hälfte davon – daher der Faktor 2 im Nenner. Multipliziert man dies wiederum mit dem Lagerkostensatz, so erhält man die jährlichen Lagerhaltungskosten.
Nehmen wir unser Beispiel von vorher: Wir bestellen immer 50 Stück auf einmal, der Preis des Artikels betrage 20 € und der Lagerkostensatz 15%, dann kommen wir auf jährliche Lagerhaltungskosten in Höhe von 75 €. In Abbildung 2 erfolgt eine grafische Darstellung: Die jährlichen Lagerhaltungskosten steigen proportional mit der Bestellmenge an.
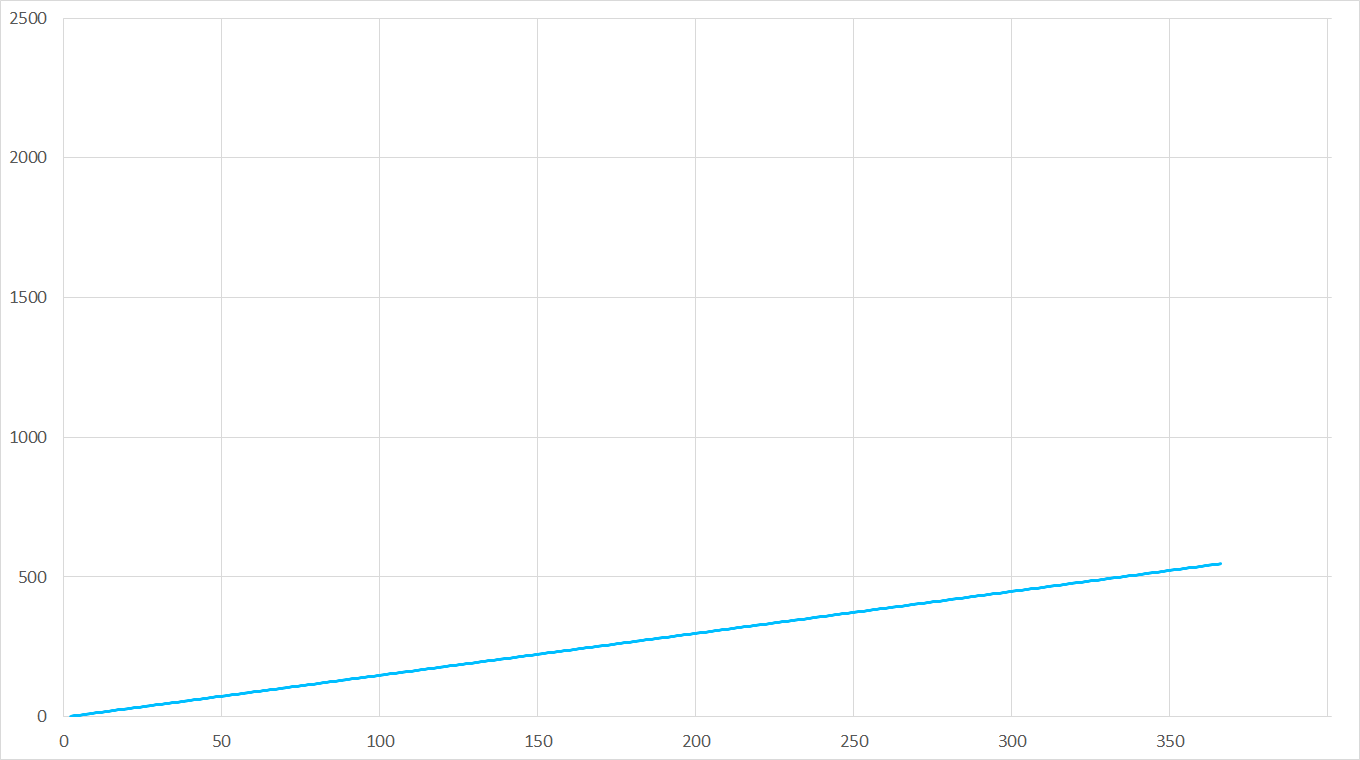
Abbildung 2: Jährliche Lagerhaltungskosten in Abhängigkeit von der Bestellmenge
Schritt 3: Zusammenfügen der Erkenntnisse
Fassen wir die bisher gewonnen Erkenntnisse zusammen: Wir haben anfangs die jährlichen Kosten pro Bestellung ausgerechnet – also das Produkt aus der Anzahl der Bestellungen pro Jahr und den Kosten pro Bestellung. Zudem kennen wir die jährlichen Lagerhaltungskosten, deren Berechnung etwas komplizierter war und einiger Annahmen bedurfte. Die jährlichen Bestellkosten \( K(x) \), deren Minimum wir suchen, entspricht der Summe aus jährlichen Bestellkosten und jährlichen Lagerkosten, also \[ K(x) = \frac{j}{x} \cdot B + \frac{x \cdot P \cdot l}{2} \]
Wir suchen die optimale Bestellmenge – also den Wert, bei dem die Kosten \( K(x) \) minimal sind. Das ist dann der Fall, wenn die erste Ableitung gleich Null ist, also \( K'(x) = 0 \). \begin{align} K'(x) &= - \frac{j}{x^2} \cdot B + \frac{P \cdot l}{2} \\ &\stackrel{!}{=} 0 \end{align}
Als nächstes lösen wir diese Gleichung nach x auf. \[ x = \pm \sqrt{\frac{2 \cdot j \cdot B}{P \cdot l}} \]
Nur die positive Lösung der Gleichung ist sinnvoll. Die minimalen jährlichen Bestellkosten ergeben sich also bei der Menge \[ x_{_{_{K = min}}} = \sqrt{\frac{2 \cdot j \cdot B}{P \cdot l}} \]
Mit unseren Beispielzahlen von zuvor wäre \( x = 141 \), man würde also jeweils eine Menge bestellen, die achteinhalb Monate lang reichen würde. In Abbildung 3 erfolgt die grafische Darstellung: Die dargestellte Kurve ist die Summe der beiden Kurven aus Abbildung 1 und Abbildung 2.
Die Formel ist erstaunlich einfach. Kennt man die Parameter \(j\), \(B\), \(P\) und \(l\), dann lässt sich die optimale Bestellmenge sehr zügig berechnen. Dennoch wird diese Formel im Einkauf von mittelständischen Unternehmen so gut wie nie angewendet. Es sind zu viele realitätsferne Angaben nötig, um auf das Ergebnis zu kommen, wie beispielsweise:
- Die Kosten für die Lagerhaltung hängen vom Preis des Artikels ab, nicht jedoch von dessen Abmaßen.
- Der Preis des Artikels ist unabhängig von der Bestellmenge – in der Regel sinkt der Preis aber mit der bestellten Menge (es sei denn, ein Mengenkontrakt wäre vorhanden).
- Der Jahresbedarf des Artikels wird konstant über die Zeit verbraucht.
- Der Kapitalzinssatz ist konstant.
- Die Bestellkosten sind konstant und unabhängig von der Menge.
- Es gibt keinen Mindestbestand.
Darüber hinaus gibt es einige Punkte, die überhaupt nicht berücksichtigt werden. Welche das sind und wie Sie stattdessen vorgehen sollten, erfahren Sie in meinen Schulungen.

Abbildung 3: Jährliche Bestellkosten in Abhängigkeit von der Bestellmenge

